Triangle Inequality Theorem Lesson
What is the Triangle Inequality Theorem?
The triangle inequality theorem tells us that:
The sum of two sides of a triangle must be greater than the third side.
This theorem can be used to prove if a combination of three triangle side lengths is possible. See the image below for an illustration of the triangle inequality theorem.
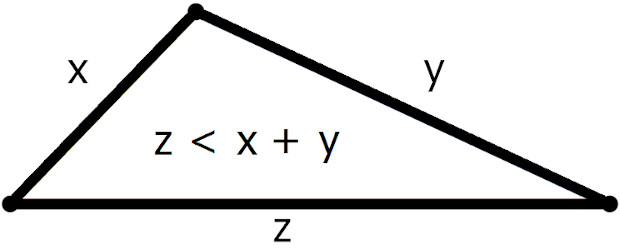
INTRODUCING

Triangle Inequality Theorem Example Problem
Referencing sides x, y, and z in the image from the above section, use the triangle inequality theorem to eliminate impossible triangle side length combinations from the following list.
- x = 2, y = 3, z = 5
- x = 5, y = 12, z = 13
- x = 3, y = 4, z = 5
- x = 12, y = 13, z = 27
- x = 2, y = 9, z = 12
Solution:
Side length combinations #1, #4, and #5 do not satisfy the requirements of the triangle inequality theorem and therefore are not possible.

