Related Content
Programmers and Teachers:
Nikkolas K.
Tutor and degreed Aerospace Engineer
Pythagorean Theorem Calculator
The hypotenuse and triangle automatically calculate when you input a and b below.
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Pythagorean Theorem Lesson
Lesson Contents
What is the Pythagorean Theorem?
The Pythagorean theorem gives us the relationship between the two legs (the shorter sides that form the right angle) of a right triangle and its hypotenuse (the longer, diagonal side). The formula is given as:
Where a and b are the legs and c is the hypotenuse. There is a variation of the Pythagorean theorem formula known as the distance formula which allows us to find the distance between two points.
How to Hand Calculate a Hypotenuse
To solve for any of three sides in a right triangle, we simply plug two of the known sides into the Pythagorean theorem formula. Let’s go through an example of this together.
A right triangle has a hypotenuse length of 5 and one of its legs has a length of 3. What is the length of the other leg?
1.) Let’s plug the two known sides into the Pythagorean Theorem formula √(a2 + b2) = c and then solve for b.
2.) √(32 + b2) = 5
3.) √(9 + b2)2 = 52
4.) 9 + b2 = 25
5.) b2 = 16
6.) b = 4
7.) The other leg of the right triangle has a length of 4.
How the Calculator Works
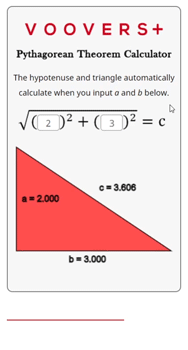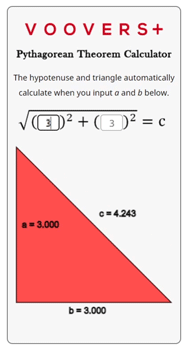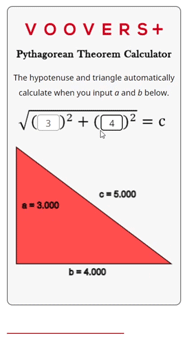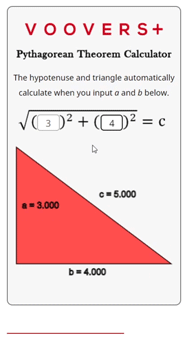
The calculator on this page is written in the programming language JavaScript. The JavaScript code runs in your internet browser continuously which is why the hypotenuse and triangle automatically update when the inputs change.
The code itself uses the Pythagorean theorem formula that is given in the lesson above. The inputs for a and b are squared, then added, and finally the square root of that sum is taken. This output is rounded to the fifth significant digit and displayed as the result for c.
The triangle is drawn by using a scaled version of the three side lengths. It draws lines along a path that uses the scaled side lengths as Cartesian coordinates. The side lengths are rounded to four significant digits and displayed next to their corresponding side.