What is a Tangent Line?

A tangent line is a line that coincides with a function's curve at a single specified point with a slope that represents the instantaneous rate of change at that point.

This basically means that the tangent line shows us how a function/curve is changing at a point. For example, let's take a look at the parabolic function f(x) = x² as seen below:

In Figure 1, the slope of the line at x = -1 is -2. This means that at the point x = -1, the curve is moving in the negative direction. In other words, the value of y is changing at a rate of -2 at x = -1.

Alternatively, let's take a look at the same parabolic function f(x) = x² with a tangent line at x = 1:

In Figure 2, the slope of the line at x = 1 is 2. This means that at the point x = 1, the curve is moving in the positive direction. In other words, the value of y is changing at a rate of 2 at x = 1.

Why do we Learn About Tangent Lines?

The utility of tangent lines appears throughout various areas in our lives. A common example of this would be our usage of electrical energy to power our homes.

The energy used in our homes is measured in kWh, or kilowatt-hour(s). How does this relate to power? Power is the rate of energy consumption (amount of energy consumed per unit time). In this case, power is measured in kW, or kilowatt(s).

So if you powered a 1500 W (1.5 kW) space heater for two hours, you would consume 3 kWh of energy.

If you had a graph of the energy usage of a household (in kWh) over a period of time, you could use tangent lines to approximate the power usage at a specific time (in kW).

By drawing a line that is tangent to the curve at a specific time and estimating its slope, you will get an approximation of the power at that point in time since the slope of the tangent line is related to the instantaneous rate of change of the plotted curve at a specific point.

How to Find the Equation of a Tangent Line

The steps to finding the equation of a tangent line are as follows:

1. Plug the given x value (x₀) into the given function f(x). This will yield the y value (y₀) at the specified x coordinate point.
2. Take the derivative of f(x) to get f'(x). Then, plug the given x value (x₀) into f'(x) to get the slope (m).
3. Plug the values for x₀, y₀, and m into the Point-slope form formula found below and simplify.

$$y - y_{0} = m(x - x_{0})$$

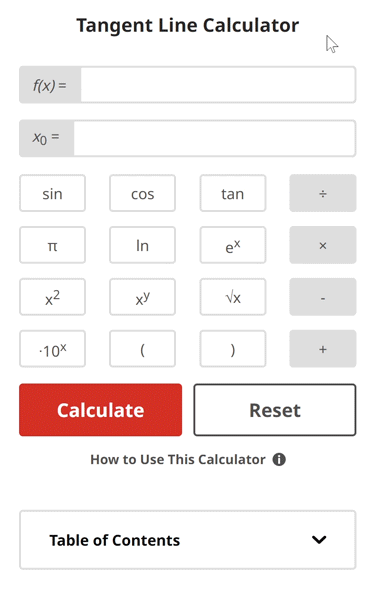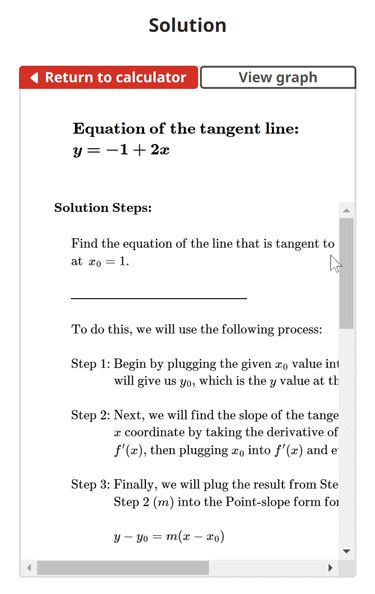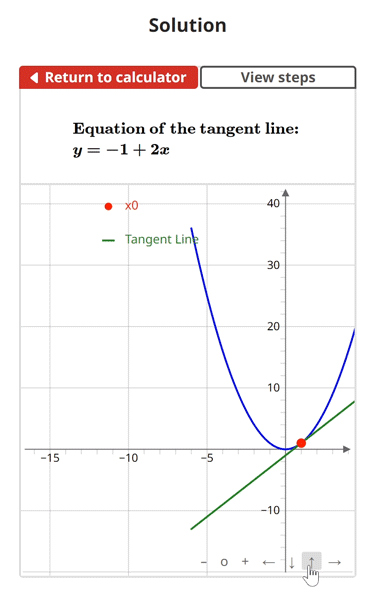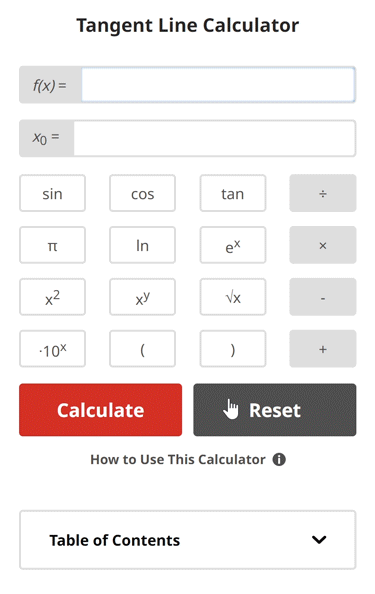
Tangent Line Example Problem

$$\begin{align}& \textbf{Solution Steps:} \\ \\ & \hspace{3ex} \text{Find the equation of the line that is tangent to } \, f(x) = x^2\\ & \hspace{3ex} \text{at } \, x_{0} = 1\text{.} \\ \\ & \hspace{3ex} \rule{6cm}{0.8pt} \\ \\ & \hspace{3ex} \text{To do this, we will use the following process:} \\ \\ & \hspace{3ex} \text{Step 1: Begin by plugging the given } x_{0} \text{ value into the given function } f(x) \text{. This} \\ & \hspace{10.5ex} \text{will give us } y_{0} \text{, which is the } y \text{ value at the given } x \text{ coordinate point.} \\ \\ & \hspace{3ex} \text{Step 2: Next, we will find the slope of the tangent line (} m \text{) at the given} \\ & \hspace{10.5ex} x \text{ coordinate by taking the derivative of the given function } f(x) \text{ to get} \\ & \hspace{10.5ex} f'(x) \text{, then plugging } x_{0} \text{ into } f'(x) \text{ and evaluating.} \\ \\ & \hspace{3ex} \text{Step 3: Finally, we will plug the result from Step 1 (} y_{0} \text{) and the result from} \\ & \hspace{10.5ex} \text{Step 2 (} m \text{) into the Point-slope form formula shown below:} \\ \\ & \hspace{10.5ex} y - y_{0} = m(x - x_{0}) \\ \\ & \hspace{3ex} \rule{6cm}{0.8pt}\\ \\ & \hspace{3ex} \text{1.) Let's begin by finding } y_{0} \text{ by plugging } x_{0} \text{ into } \, f(x) = x^2\text{:} \\ \\ & \hspace{6.5ex} \Longrightarrow y_{0} = f(x_{0}) \\ \\ & \hspace{6.5ex} \Longrightarrow f(x_{0}) = \left(1\right)^2\\ \\ & \hspace{6.5ex} \Longrightarrow y_{0} = \boxed{1}\\ \\ & \hspace{3ex} \text{2.) Next, let's find the slope of the tangent line (} m \text{):} \\ \\ & \hspace{6.5ex} \text{2.1) We will start by taking the derivative of } f(x) \text{ to get } f'(x) \text{:} \\ \\ & \hspace{11ex} \Longrightarrow f'(x) = 2 x\\ \\ & \hspace{6.5ex} \text{2.2) Next, we will plug } x_{0} \text{ into } f'(x) \text{ (found in Step 2.1) to get the slope of} \\ & \hspace{11ex} \text{the tangent line (} m \text{):} \\ \\ & \hspace{11ex} \Longrightarrow m = f'(x_{0}) \\ \\ & \hspace{11ex} \Longrightarrow f'(x) = 2 x\\ \\ & \hspace{11ex} \Longrightarrow f'(x_{0}) = 2 (1)\\ \\ & \hspace{11ex} \Longrightarrow m = \boxed{2}\\ \\ & \hspace{3ex} \text{3.) Finally, let's plug } x_{0} \text{, } y_{0} \text{, and } m \text{ into the Point-slope form equation and} \\ & \hspace{6.5ex} \text{simplify to get the equation of the tangent line:} \\ \\ & \hspace{6.5ex} \Longrightarrow y - y_{0} = m(x - x_{0}) \\ \\ & \hspace{6.5ex} \Longrightarrow y - (1) = (2)(x - (1)) \\ \\ & \hspace{6.5ex} \Longrightarrow y = - 1 + 2 x\\ \\ & \hspace{3ex} \text{Therefore, the equation of the tangent line is:} \\ & \hspace{3ex} \boxed{\boxed{y = - 1 + 2 x}}\\ & \end{align}$$

How the Calculator Works

The Tangent Line Calculator consists of HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

HTML serves as the framework for the calculator. The calculator, solution steps field, and graph are all defined and named using HTML.

CSS is used to style all of the designated HTML elements. This includes, but is not limited to, the color of the calculator buttons, the font style of the text, and the size of the input fields

Once the interface is present and styled on the page, JS is used to add functionality to the calculator. In addition to handling all of the calculations performed by the calculator, JS also performs dynamic interface controls such as resetting the calculator inputs and automatically typing in mathematical symbols like "π" when the user presses the corresponding key on the calculator's keypad.

These different languages work together to produce an easy and intuitive way to learn about finding the equation of a tangent line.