What is Synthetic Division?

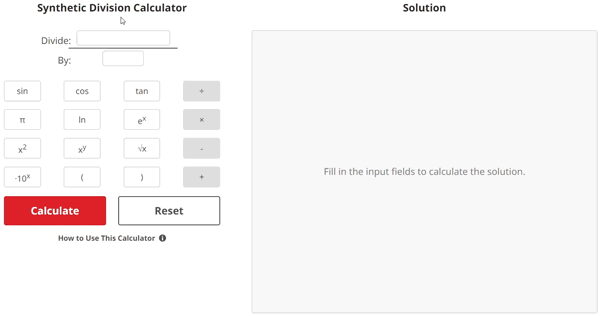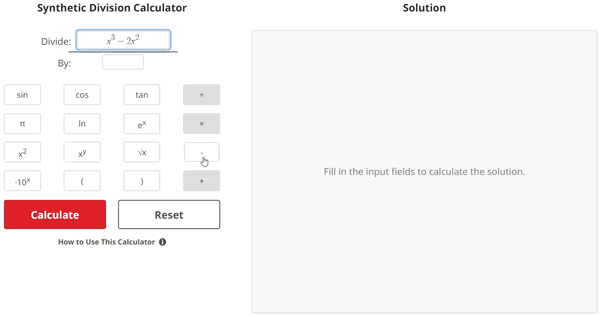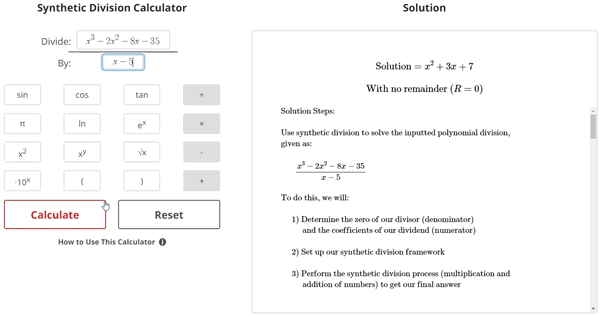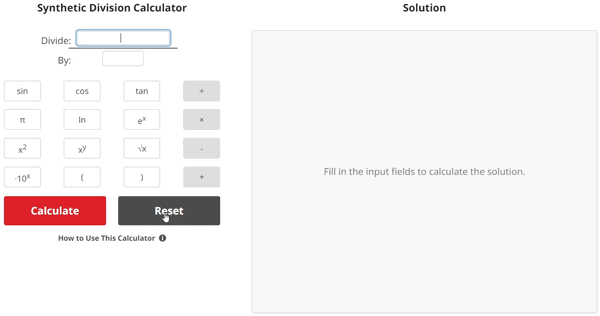
Synthetic division is a simplified form of polynomial division. It allows us to divide a polynomial of second or higher degree, such as x³ - 2x² - 8x - 35, by a first-degree polynomial (also called a linear factor), such as x - 5.

As seen in the image above, synthetic division uses an L-shaped division line to guide us during our calculations. Once we convert our division polynomials to the correct format for synthetic division, we simply repeat multiplication and addition to find the quotient.

Compared to long division, synthetic division is more restricted in use as we must be dividing by a first-degree polynomial (also called a linear factor), but, it can often be more convenient and easier to use.

Why do we Learn About Synthetic Division?

Since synthetic division allows us to divide polynomials and therefore find the zeros (roots) of polynomials, it has countless real-world uses. Let's check out just one of these many uses: predicting storm patterns to keep people safe from dangerous weather.

Meteorologists often use polynomials to model weather patterns. Some of these polynomials approximate when and where severe storms may occur and impact the people who live there, who need to have accurate warning far in advance to prepare for potentially dangerous weather.

A way to use these approximation polynomials for storm predictions is to solve the polynomial by finding its zeros (roots). Fortunately, synthetic division can simplify polynomials and provide us a direct path to finding these zeros (roots).

By dividing a second-degree or higher polynomial by a first-degree polynomial like we do with synthetic division, we can determine the quotient which is often another first-degree polynomial.

The quotient polynomial and polynomial we divided by (called the divisor or denominator) form a factored version of the original approximation polynomial. Because it is now factored, we can easily find the zeros (roots) of the original polynomial by setting each of the first-degree, factored polynomials equal to zero and solving for x.

Once we have found the x solutions of these factored polynomials, we now know the solutions to the polynomial for predicting the potential storms! By using synthetic division, we have potentially helped people stay out of harm's way.

How to do a Synthetic Division Calculation (Example Problem 1)

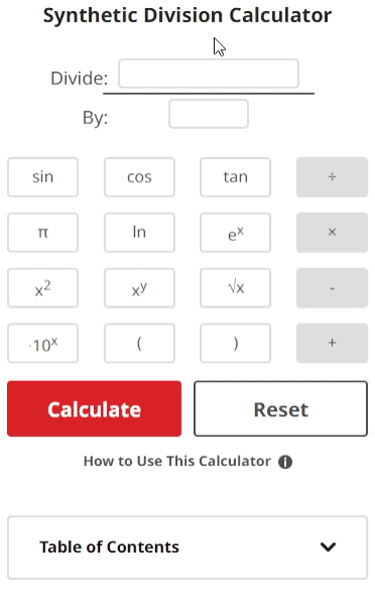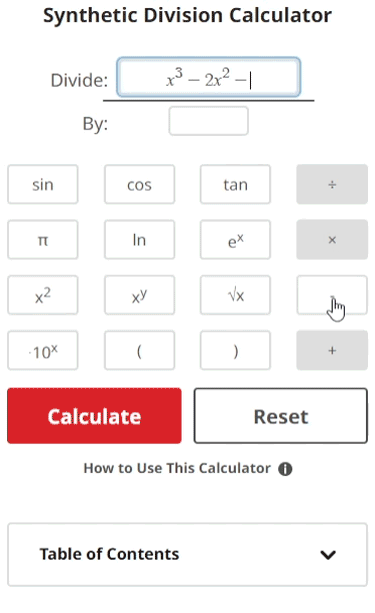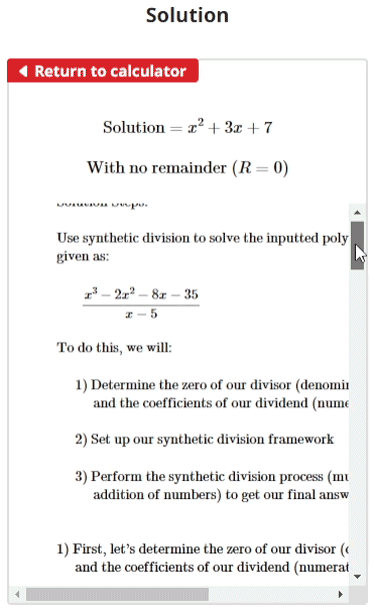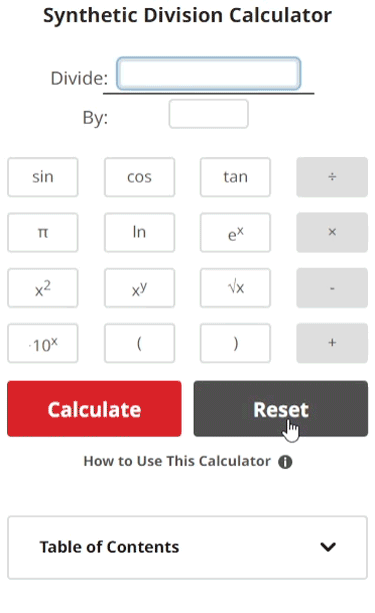
$$\begin{align}& \hspace{2ex} \text{Use synthetic division to solve the polynomial division problem:} \\ \\ & \hspace{6ex} \frac{x^3-2x^2-8x-35}{x-5}\\ \\ & \hspace{2ex} \text{To do this, we will:} \\ \\ & \hspace{5ex} \text{1) Determine the zero of our divisor (denominator)} \\ & \hspace{8ex} \text{and the coefficients of our dividend (numerator)} \\ \\ & \hspace{5ex} \text{2) Set up our synthetic division framework} \\ \\ & \hspace{5ex} \text{3) Perform the synthetic division process (multiplication and} \\ & \hspace{8ex} \text{addition of numbers) to get our final answer}\\ \\ \\ & \hspace{2ex} \text{1) First, let's determine the zero of our divisor (denominator)} \\ & \hspace{5ex} \text{and the coefficients of our dividend (numerator).}\\ \\ & \hspace{4ex} \text{1.1) Our divisor (denominator) is given as: } \;x-5\\ \\ & \hspace{9ex} \text{Setting it equal to zero and solving for } x \text{, we get:} \\ \\ & \hspace{10ex}x-5 = 0 \; \Longrightarrow \; x = 5\\ \\ & \hspace{10ex} \boxed{\text{Divisor (denominator) zero } = 5}\\ \\ & \hspace{4ex} \text{1.2) Our dividend (numerator) polynomial is given as: } \;x^3-2x^2-8x-35\\ \\ & \hspace{9ex} \text{Our coefficients in order from their term's} \\ & \hspace{9ex} \text{greatest degree to least degree are as follows:}\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{3} \text{ term is }1\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{2} \text{ term is }-2\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{1} \text{ term is }-8\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{0} \text{ term is }-35\\ \\ & \hspace{10ex} \boxed{ \text{Dividend (numerator) coefficients} = 1\text{, }-2\text{, }-8\text{, }-35}\\ \\ \\ & \hspace{2ex} \text{2) Now, let's set up our synthetic division framework. To do this, we will:} \\ & \hspace{6ex} \bullet \text{Draw a sideways L-shaped division line} \\ & \hspace{6ex} \bullet \text{Write the dividend (numerator) coefficients inside the L and} \\ & \hspace{8ex} \text{in order from their term's greatest degree to least degree} \\ & \hspace{6ex} \bullet \text{Write the divisor (denominator) root outside the L and to the left} \\ \\ & \hspace{5ex} \text{Doing so, we get:} \\ \\ & \hspace{10ex}\begin{array}{c}5\end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\ \hline \end{array}\\ \\ & \hspace{5ex} \text{To finish setting up the framework, let's drop the} \\ & \hspace{5ex} \text{first dividend (numerator) coefficient down to} \\ & \hspace{5ex} \text{just below the bottom line. Doing so, we get:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1\end{array}\\ \\ \\ & \hspace{2ex} \text{3) Finally, let's use the synthetic division process to determine our answer.} \\\\[-1em] & \hspace{4ex} \text{3.1a) Multiplying the bottom right number } (1) \text{ by the top left} \\ & \hspace{10ex} \text{number } (5) \text{, we get: } \; (1) \cdot (5) =5\\ \\ & \hspace{10ex} \text{After inserting the product } (5) \text{ up and to the right} \\ & \hspace{10ex} \text{of the bottom right number by one slot, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\[-2em] & \hspace{4ex} \text{3.1b) Vertically adding the new product } (5) \text{ to the coefficient directly} \\ & \hspace{10ex} \text{above it } (-2) \text{, we get: } \; (5) + (-2) =3\\ \\ & \hspace{10ex} \text{After inserting that sum directly below, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1&3\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\ & \hspace{4ex} \text{We will repeat the previous two operations (a & b) until our bottom row} \\ & \hspace{4ex} \text{has the same amount of numbers as the dividend has coefficients } (4) \\ \\\\[-1em] & \hspace{4ex} \text{3.2a) Multiplying the bottom right number } (3) \text{ by the top left} \\ & \hspace{10ex} \text{number } (5) \text{, we get: } \; (3) \cdot (5) =15\\ \\ & \hspace{10ex} \text{After inserting the product } (15) \text{ up and to the right} \\ & \hspace{10ex} \text{of the bottom right number by one slot, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5&15\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1&3\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\[-2em] & \hspace{4ex} \text{3.2b) Vertically adding the new product } (15) \text{ to the coefficient directly} \\ & \hspace{10ex} \text{above it } (-8) \text{, we get: } \; (15) + (-8) =7\\ \\ & \hspace{10ex} \text{After inserting that sum directly below, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5&15\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1&3&7\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\[-1em] & \hspace{4ex} \text{3.3a) Multiplying the bottom right number } (7) \text{ by the top left} \\ & \hspace{10ex} \text{number } (5) \text{, we get: } \; (7) \cdot (5) =35\\ \\ & \hspace{10ex} \text{After inserting the product } (35) \text{ up and to the right} \\ & \hspace{10ex} \text{of the bottom right number by one slot, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5&15&35\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1&3&7\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\[-2em] & \hspace{4ex} \text{3.3b) Vertically adding the new product } (35) \text{ to the coefficient directly} \\ & \hspace{10ex} \text{above it } (-35) \text{, we get: } \; (35) + (-35) =0\\ \\ & \hspace{10ex} \text{After inserting that sum directly below, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}5\\ \phantom{1} \end{array} \; \begin{array}{|rrrr}1&-2&-8&-35\\\phantom{1}&5&15&35\\ \hline \end{array} \\ & \begin{array}{rrrr}\phantom{5} \hspace{9.5ex} &1&3&7&0\\\phantom{5} \hspace{9.5ex}& \phantom{1}& \phantom{-2}& \phantom{-8}& \phantom{-35}\\\phantom{5} \hspace{9.5ex}& \phantom{\phantom{1}}& \phantom{5}& \phantom{15}& \phantom{35}\end{array}\\[-1em] & \hspace{4ex} \text{We have now reached the end of the synthetic division process.} \\ & \hspace{4ex}\text{Since the final number at the bottom right is zero, there is no remainder.} \\ \\ & \hspace{4ex}\text{Our newly calculated bottom row of numbers (except for the last one, which} \\ & \hspace{4ex} \text{is the remainder) divided by the leading coefficient for } x \text{ (}1 \text{) from our original} \\ & \hspace{4ex} \text{divisor (denominator) will create the answer (quotient) polynomial.} \\ \\ & \hspace{5ex} \text{Answer (quotient) coefficients: } \;1, \:3, \:7\\ & \hspace{5ex} \text{Made into a polynomial: } \;x^{2}+ 3x^{}+ 7\\ & \hspace{5ex} \text{Divided by the divisor's } x \text{ coefficient (}1\text{): } \;x^{2}+ 3x^{}+ 7\\ \\ & \hspace{5ex} \boxed{ \text{Final answer (quotient)} = \boxed{x^{2}+ 3x^{}+ 7}} \\ & \hspace{5ex} \boxed{ \text{With no remainder } (R = 0)}\end{align}$$

How to do a Synthetic Division Calculation (Example Problem 2)

$$\begin{align}& \hspace{2ex} \text{Use synthetic division to solve the polynomial division problem:} \\ \\ & \hspace{6ex} \frac{2x^2+2x-14}{2x+6}\\ \\ & \hspace{2ex} \text{To do this, we will:} \\ \\ & \hspace{5ex} \text{1) Determine the zero of our divisor (denominator)} \\ & \hspace{8ex} \text{and the coefficients of our dividend (numerator)} \\ \\ & \hspace{5ex} \text{2) Set up our synthetic division framework} \\ \\ & \hspace{5ex} \text{3) Perform the synthetic division process (multiplication and} \\ & \hspace{8ex} \text{addition of numbers) to get our final answer}\\ \\ \\ & \hspace{2ex} \text{1) First, let's determine the zero of our divisor (denominator)} \\ & \hspace{5ex} \text{and the coefficients of our dividend (numerator).}\\ \\ & \hspace{4ex} \text{1.1) Our divisor (denominator) is given as: } \;2x+6\\ \\ & \hspace{9ex} \text{Setting it equal to zero and solving for } x \text{, we get:} \\ \\ & \hspace{10ex}2x+6 = 0 \; \Longrightarrow \; x = -3\\ \\ & \hspace{10ex} \boxed{\text{Divisor (denominator) zero } = -3}\\ \\ & \hspace{4ex} \text{1.2) Our dividend (numerator) polynomial is given as: } \;2x^2+2x-14\\ \\ & \hspace{9ex} \text{Our coefficients in order from their term's} \\ & \hspace{9ex} \text{greatest degree to least degree are as follows:}\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{2} \text{ term is }2\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{1} \text{ term is }2\\ & \hspace{10ex} \bullet \text{The coefficient of the } x^{0} \text{ term is }-14\\ \\ & \hspace{10ex} \boxed{ \text{Dividend (numerator) coefficients} = 2\text{, }2\text{, }-14}\\ \\ \\ & \hspace{2ex} \text{2) Now, let's set up our synthetic division framework. To do this, we will:} \\ & \hspace{6ex} \bullet \text{Draw a sideways L-shaped division line} \\ & \hspace{6ex} \bullet \text{Write the dividend (numerator) coefficients inside the L and} \\ & \hspace{8ex} \text{in order from their term's greatest degree to least degree} \\ & \hspace{6ex} \bullet \text{Write the divisor (denominator) root outside the L and to the left} \\ \\ & \hspace{5ex} \text{Doing so, we get:} \\ \\ & \hspace{10ex}\begin{array}{c}-3\end{array} \; \begin{array}{|rrr}2&2&-14\\ \hline \end{array}\\ \\ & \hspace{5ex} \text{To finish setting up the framework, let's drop the} \\ & \hspace{5ex} \text{first dividend (numerator) coefficient down to} \\ & \hspace{5ex} \text{just below the bottom line. Doing so, we get:}\\ \\ & \hspace{10ex} \begin{array}{c}-3\\ \phantom{1} \end{array} \; \begin{array}{|rrr}2&2&-14\\\phantom{2}\\ \hline \end{array} \\ & \begin{array}{rrr}\phantom{-3} \hspace{9.5ex} &2\end{array}\\ \\ \\ & \hspace{2ex} \text{3) Finally, let's use the synthetic division process to determine our answer.} \\\\[-1em] & \hspace{4ex} \text{3.1a) Multiplying the bottom right number } (2) \text{ by the top left} \\ & \hspace{10ex} \text{number } (-3) \text{, we get: } \; (2) \cdot (-3) =-6\\ \\ & \hspace{10ex} \text{After inserting the product } (-6) \text{ up and to the right} \\ & \hspace{10ex} \text{of the bottom right number by one slot, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}-3\\ \phantom{1} \end{array} \; \begin{array}{|rrr}2&2&-14\\\phantom{2}&-6\\ \hline \end{array} \\ & \begin{array}{rrr}\phantom{-3} \hspace{9.5ex} &2\\\phantom{-3} \hspace{9.5ex}& \phantom{2}& \phantom{2}& \phantom{-14}\\\phantom{-3} \hspace{9.5ex}& \phantom{\phantom{2}}& \phantom{-6}& \phantom{12}\end{array}\\[-2em] & \hspace{4ex} \text{3.1b) Vertically adding the new product } (-6) \text{ to the coefficient directly} \\ & \hspace{10ex} \text{above it } (2) \text{, we get: } \; (-6) + (2) =-4\\ \\ & \hspace{10ex} \text{After inserting that sum directly below, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}-3\\ \phantom{1} \end{array} \; \begin{array}{|rrr}2&2&-14\\\phantom{2}&-6\\ \hline \end{array} \\ & \begin{array}{rrr}\phantom{-3} \hspace{9.5ex} &2&-4\\\phantom{-3} \hspace{9.5ex}& \phantom{2}& \phantom{2}& \phantom{-14}\\\phantom{-3} \hspace{9.5ex}& \phantom{\phantom{2}}& \phantom{-6}& \phantom{12}\end{array}\\ & \hspace{4ex} \text{We will repeat the previous two operations (a & b) until our bottom row} \\ & \hspace{4ex} \text{has the same amount of numbers as the dividend has coefficients } (3) \\ \\\\[-1em] & \hspace{4ex} \text{3.2a) Multiplying the bottom right number } (-4) \text{ by the top left} \\ & \hspace{10ex} \text{number } (-3) \text{, we get: } \; (-4) \cdot (-3) =12\\ \\ & \hspace{10ex} \text{After inserting the product } (12) \text{ up and to the right} \\ & \hspace{10ex} \text{of the bottom right number by one slot, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}-3\\ \phantom{1} \end{array} \; \begin{array}{|rrr}2&2&-14\\\phantom{2}&-6&12\\ \hline \end{array} \\ & \begin{array}{rrr}\phantom{-3} \hspace{9.5ex} &2&-4\\\phantom{-3} \hspace{9.5ex}& \phantom{2}& \phantom{2}& \phantom{-14}\\\phantom{-3} \hspace{9.5ex}& \phantom{\phantom{2}}& \phantom{-6}& \phantom{12}\end{array}\\[-2em] & \hspace{4ex} \text{3.2b) Vertically adding the new product } (12) \text{ to the coefficient directly} \\ & \hspace{10ex} \text{above it } (-14) \text{, we get: } \; (12) + (-14) =-2\\ \\ & \hspace{10ex} \text{After inserting that sum directly below, we now have:}\\ \\ & \hspace{10ex} \begin{array}{c}-3\\ \phantom{1} \end{array} \; \begin{array}{|rrr}2&2&-14\\\phantom{2}&-6&12\\ \hline \end{array} \\ & \begin{array}{rrr}\phantom{-3} \hspace{9.5ex} &2&-4&-2\\\phantom{-3} \hspace{9.5ex}& \phantom{2}& \phantom{2}& \phantom{-14}\\\phantom{-3} \hspace{9.5ex}& \phantom{\phantom{2}}& \phantom{-6}& \phantom{12}\end{array}\\[-1em] & \hspace{4ex} \text{We have now reached the end of the synthetic division process.} \\ & \hspace{4ex}\text{Since the final number at the bottom right is not zero, there} \\ & \hspace{4ex} \text{is a remainder. The remainder is the bottom right number } (-2) \text{.} \\ \\ & \hspace{4ex}\text{Our newly calculated bottom row of numbers (except for the last one, which} \\ & \hspace{4ex} \text{is the remainder) divided by the leading coefficient for } x \text{ (}2 \text{) from our original} \\ & \hspace{4ex} \text{divisor (denominator) will create the answer (quotient) polynomial.} \\ \\ & \hspace{5ex} \text{Answer (quotient) coefficients: } \;2, \:-4\\ & \hspace{5ex} \text{Made into a polynomial: } \;2x^{}-4\\ & \hspace{5ex} \text{Divided by the divisor's } x \text{ coefficient (}2\text{): } \;\frac{2x^{}-4}{2} \\ \\ & \hspace{5ex} \boxed{ \text{Final answer (quotient)} = \boxed{\frac{2x^{}-4}{2}}} \\ & \hspace{5ex} \boxed{ \text{With a remainder of:} \; \boxed{ R = -2}}\end{align}$$

How the Calculator Works

The Synthetic Division Calculator on this page is written in the programming languages HTML, CSS, and JS.

HTML (HyperText Markup Language) is what creates the calculator's framework. Every entity the builds up what we see with the calculator is coded as an HTML element. The HTML assigns identification names to each of these to help the CSS and JS access and modify them.

CSS (Cascading Style Sheets) controls how the HTML elements appear to us. It can move them around, color them, shape them, and even creates the animations of the buttons that we click. Without CSS, the calculator would not look as good or be as user-friendly!

JS (JavaScript) is the motor behind the scenes that makes things tick. For this calculator, the inputs are detected, calculations are performed, and errors are reported all via JS. Because JS runs naturally and efficiently in our internet browsers, the calculator can provide nearly instantaneous solutions!