In physics, projectile motion is the study of how a particle or object moves when the only force affecting it is gravity. When a projectile travels through flight, the path it follows is called the trajectory. If viewed from the side, the trajectory is a parabolic shape (called a ballistic trajectory).

Imagine throwing a ball but there is no air to cause drag force on the ball. Once it leaves your hand, the only force the ball experiences is the gravitational force. The ball is considered a projectile and will follow a ballistic trajectory.

We can hand calculate the trajectory of a projectile with the kinematic equations. After rearranging and simplifying the equations to solve for projectile motion, they are given as:
v_x = v₀cos(α)
v_y = v₀sin(α)
t = ^2v_y/_g
x = v_xt

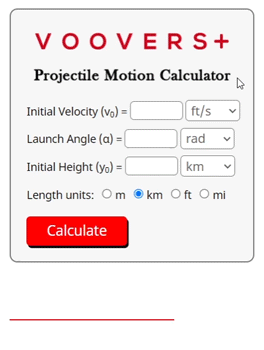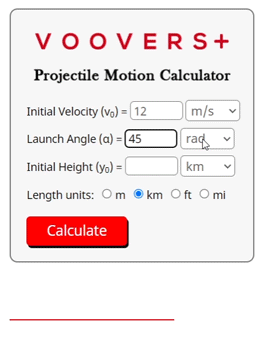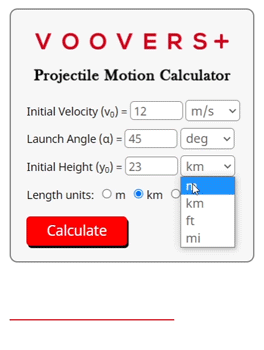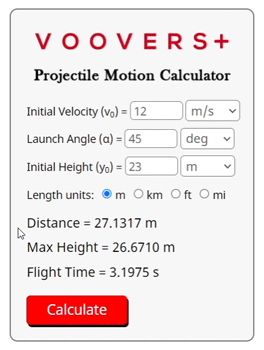
These equations are all we need to solve flight time and flight distance for a projectile that is launched from ground level (an initial height of zero). First, we plug the initial velocity (v₀) and launch angle (α) into the v_x and v_y equations. This gives us the velocity components for the x (horizontal) and y (vertical) directions.

Then, we plug v_y and gravitational acceleration (g) into the flight time (t) equation. Once we have determined flight time, we plug it into the distance (x) equation. After solving for x, we have successfully determined how far the projectile flies on its trajectory before reaching the ground.