What are Critical Points?

A critical point is a point on a given domain of a function where the function's derivative is either zero or undefined, and the function itself exists at that point.

Why do we Learn About Critical Points?

Critical points appear everywhere within physics and mathematics, and can be used to give us useful insight into what is happening in a physical phenomenon. Take projectile motion for example. Let's say we are throwing a ball up into the air at some velocity and angle above the horizon. The path of the projectile (ball), assuming constant/no drag on the projectile, will be in the shape of a parabola.

We can use critical points to determine when our ball transitions from upward flight to falling back to the Earth. In turn, we can use this information to determine the maximum ball height.

If we have a reasonably approximated equation for the vertical position of the ball with respect to time, we can take the derivative of this position equation to find the rate of change in vertical position of the ball with respect to a change in time. Then, we can solve for the point in time that the derivative equation (velocity) equals zero. This basically tells us when the ball stops moving upwards and begins falling back down.

In other words, this will let us know at what point in time the ball has reached its maximum height. We can then take that value for time, input it into our position equation, and that would tell us what the maximum height of the ball was in this case.

Another way we can use critical points is interpreting a data set. Let's say we are building a small model rocket that can deploy a parachute to safely fall back down to the ground once it has reached its maximum height.

By using an accelerometer, we can measure the acceleration that the rocket sees and use that data to automatically deploy the parachute after the rocket has reached its maximum altitude. What does this have to do with critical points?

Well, as the rocket sits on the launchpad prior to launch, the accelerometer will read a value of 1g, or one times the acceleration due to the Earth's gravity (9.81 ^m⁄_s²). On takeoff, the accelerometer will have a reading of greater than 1g as it accelerates upward. When the rocket motor burns out, the rocket will still be moving upward into the sky but it will start to slow down. When the rocket finally approaches its maximum height, the accelerometer will approach a reading of 0g as it transitions to free fall.

This would be a critical point of the position data because when the rocket transitions from upward movement to falling back to Earth, the velocity goes from a positive value (assuming upward movement is positive) to a negative velocity. If you were to look at a graph of the rocket position versus time, the point where the accelerometer approaches a reading of 0g, would be when the change in position with respect to the change in time (velocity) approaches zero.

In other words, the derivative of the position curve (velocity) would be zero at the rocket's maximum height, telling our system that it is acceptable to deploy the parachute.

How to Find the Critical Points of a Function?

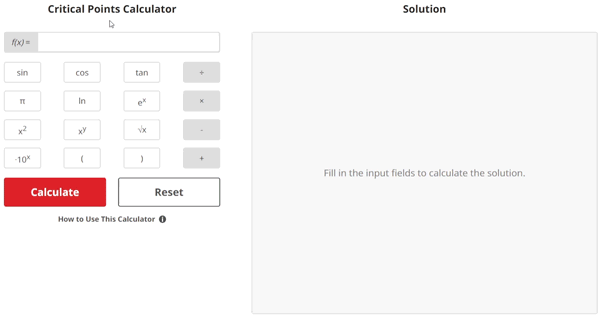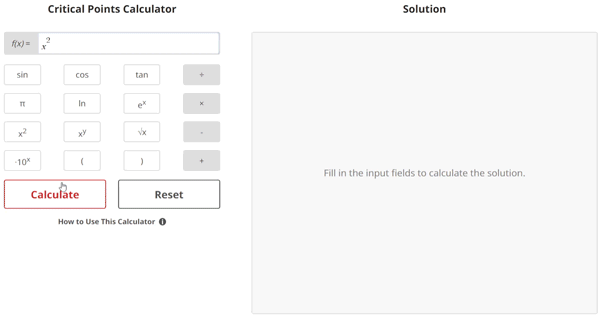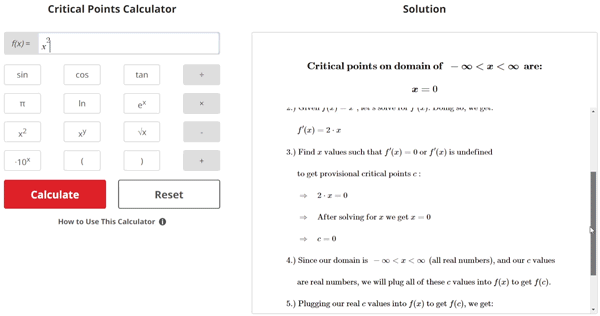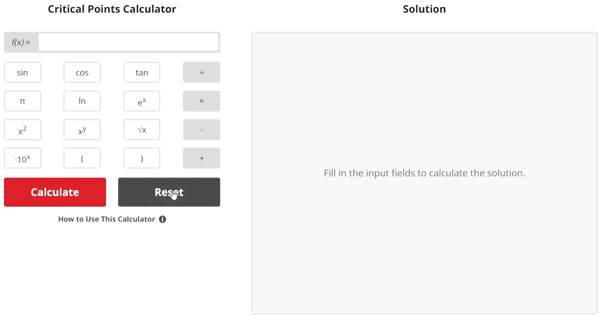
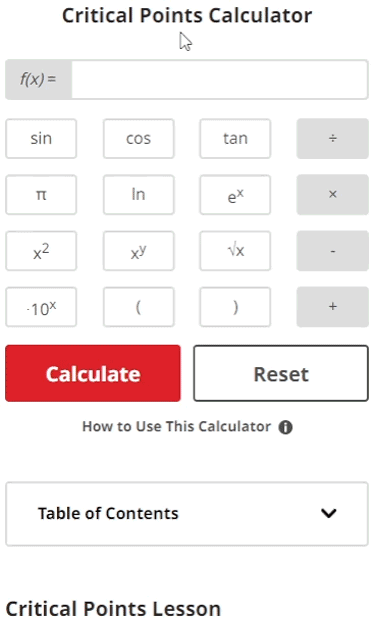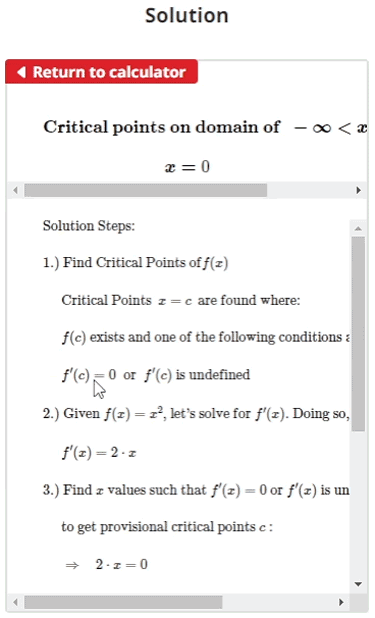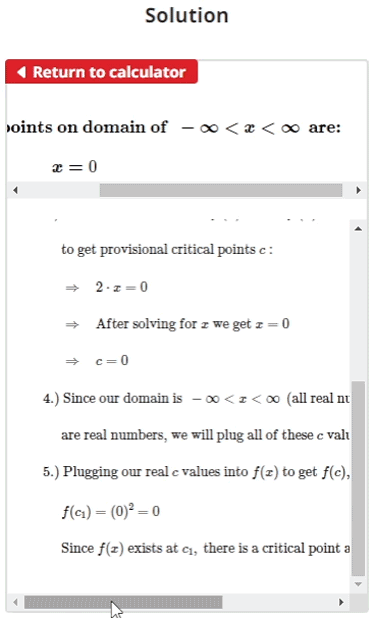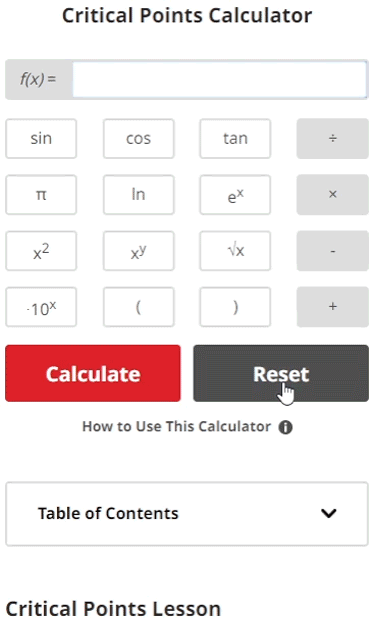
Critical points x = c are found under the following conditions:

1. f '(c) equals zero OR f '(c) is undefined
2. f(c) exists

Where c is the critical point that satisfies both conditions, f '(c) is the derivative of the input function f(x) evaluated at x = c, and f(c) is the input function f(x) evaluated at x = c.

Steps for finding the critical points of a given function f(x):

1. Take derivative of f(x) to get f '(x)
2. Find x values where f '(x) = 0 and/or where f '(x) is undefined
3. Plug the values obtained from step 2 into f(x) to test whether or not the function exists for the values found in step 2
4. The x values found in step 2 where f(x) does exist can be taken as critical points since the function exists at these points and they lie within the domain of our function f(x)

Example Problem 1

$$\begin{align}& \text{1.) Find the critical points of } f(x) = \frac{x^3}{3}-16x \\ \\ & \hspace{3ex} \text{Critical Points } \: x = c \: \text{ are found where:} \\ \\ & \hspace{3ex} f(c) \text{ exists and one of the following conditions are met:} \hspace{15ex} \\ \\ & \hspace{3ex} f'(c) = 0 \; \text{ or } \; f'(c) \text{ is undefined}\\ \\ & \text{2.) Given } f(x) = \frac{x^3}{3}-16x\text{, find } f'(x) \text{:} \\ \\ & \hspace{3ex} f'(x) ={x}^{2} - 16\\ \\ & \text{3.) Find } x \text{ values such that } f'(x) = 0 \text{ or } f'(x) \text{ is undefined } \\ \\ & \hspace{3ex} \text{to get provisional critical points } c \text{ :} \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} {x}^{2} - 16 = 0 \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} \text{After solving for } x \text{ we get } x =4,-4\\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} c =4,-4\\ \\ & \text{4.) Since our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{(all real numbers), and our } c \text{ values} \\ \\ & \hspace{3ex} \text{are real numbers, we will plug all of these } c \text{ values into } f(x) \text{ to get } f(c) \text{.}\\ \\ & \text{5.) Plugging our real } c \text{ values into } f(x) \text{ to get } f(c) \text{, we get:}\\ \\ & \hspace{3ex} f(c_{1}) = \frac{(4)^3}{3}-16(4) = -42.666666666666664\\ \\ & \hspace{3ex} \text{Since } f(x) \text { exists at } c_{1}, \text{ there is a critical point at } c_{1} \text{ = } 4\\\\ \\ & \hspace{3ex} f(c_{2}) = \frac{(-4)^3}{3}-16(-4) = 42.666666666666664\\ \\ & \hspace{3ex} \text{Since } f(x) \text { exists at } c_{2}, \text{ there is a critical point at } c_{2} \text{ = } -4\\\end{align}$$

Example Problem 2

$$\begin{align}& \text{1.) Find the critical points of } f(x) = \frac{1}{3x}-\frac{1}{6}x^2 \\ \\ & \hspace{3ex} \text{Critical Points } \: x = c \: \text{ are found where:} \\ \\ & \hspace{3ex} f(c) \text{ exists and one of the following conditions are met:} \hspace{15ex} \\ \\ & \hspace{3ex} f'(c) = 0 \; \text{ or } \; f'(c) \text{ is undefined}\\ \\ & \text{2.) Given } f(x) = \frac{1}{3x}-\frac{1}{6}x^2\text{, find } f'(x) \text{:} \\ \\ & \hspace{3ex} f'(x) =- \frac{1}{3} \cdot x - \frac{1}{3 \cdot {x}^{2}}\\ \\ & \text{3.) Find } x \text{ values such that } f'(x) = 0 \text{ or } f'(x) \text{ is undefined } \\ \\ & \hspace{3ex} \text{to get provisional critical points } c \text{ :} \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} - \frac{1}{3} \cdot x - \frac{1}{3 \cdot {x}^{2}} = 0 \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} \text{After solving for } x \text{ we get } x =-1,\frac{1}{2}i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt{3} + \frac{1}{2},0\\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} c =-1,\frac{1}{2}i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt{3} + \frac{1}{2},0\\ \\ & \text{4.) Since our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{(all real numbers), we will not plug} \\ \\ & \hspace{3ex} \text{the imaginary values back into } f(x) \text{ to find } f(c) \text{. Instead, we will proceed} \\ \\ & \hspace{3ex} \text{with only the } c \text{ values that are real numbers.}\\ \\ & \text{5.) Plugging our real } c \text{ values into } f(x) \text{ to get } f(c) \text{, we get:}\\ \\ & \hspace{3ex} f(c_{1}) = \frac{1}{3(-1)}-\frac{1}{6}(-1)^2 = -0.5\\ \\ & \hspace{3ex} \text{Since } f(x) \text { exists at } c_{1}, \text{ there is a critical point at } c_{1} \text{ = } -1\\\\ \\ & \hspace{3ex} f(c_{2}) = \frac{1}{3(0)}-\frac{1}{6}(0)^2 = \text{undefined} \\ & \hspace{3ex} \text{No critical point exists at this c value since } f(c) \text{ is not defined at this point.}\\\end{align}$$

How the Calculator Works

The Critical Points Calculator was developed using HTML, CSS, and JavaScript. The HTML portion of the code creates the framework of the calculator. This framework designates various important entities such as the calculator space itself, answer box, and the solution box.

CSS is then used to provide custom styling to the calculator and answer elements so that it is easy to read and use as needed. Everything from the clickable calculator button styling to the automated scroll bars in the solution field are styled using CSS.

For calculator functionality, JavaScript is used. This includes physical button presses, deriving the user's input function, and outputting the custom solution steps tailored to the user's inputs. When all of these components come together, we get a smooth and satisfying calculator experience that is responsive to the user's specific needs.